I recently conducted a minor survey on potential functions in the context of multi-agent systems. Collective potential functions are a common way to produce desired separation between agents in a swarm. Fig. 1 provides an illustration of one such scenario.

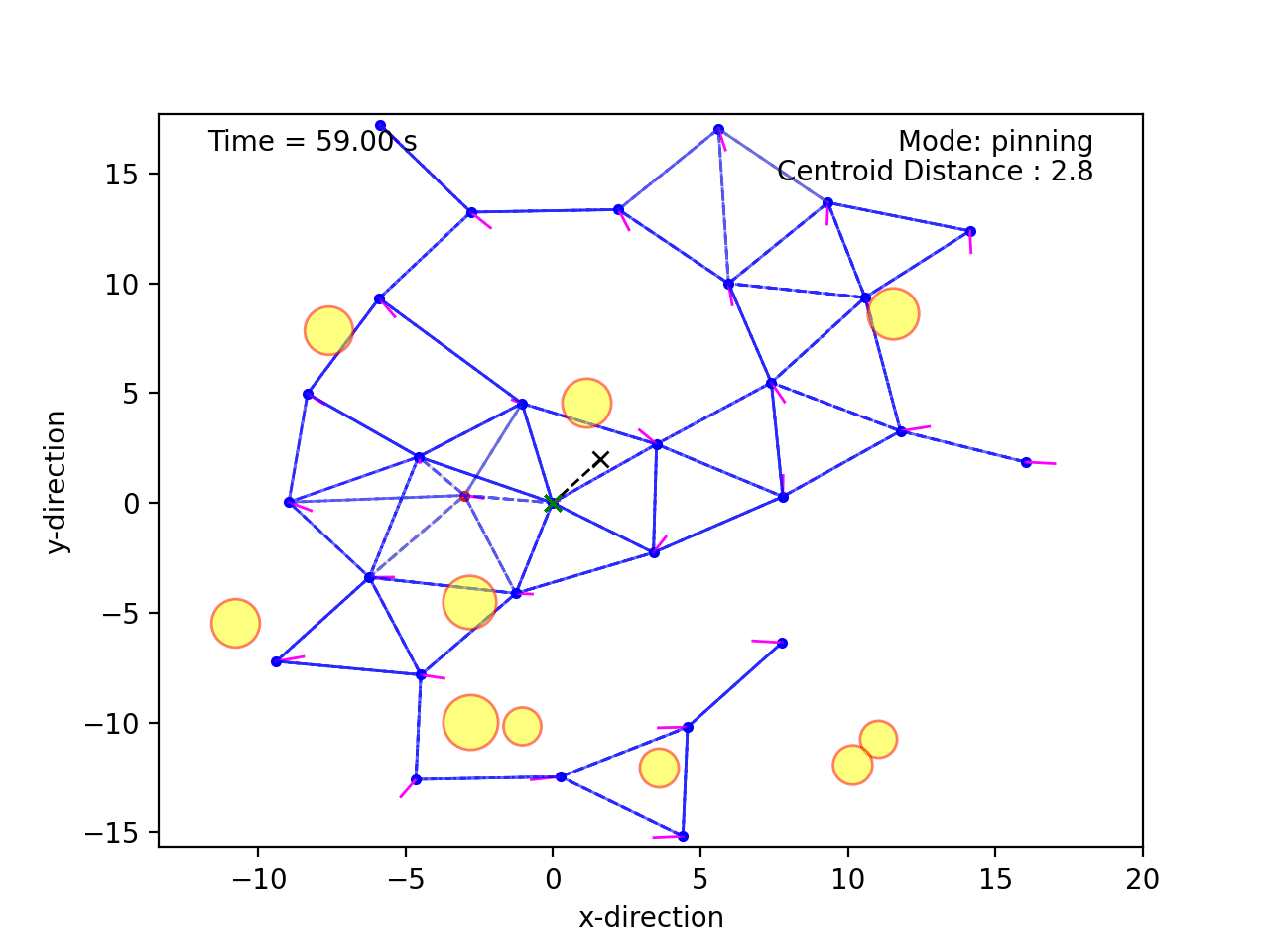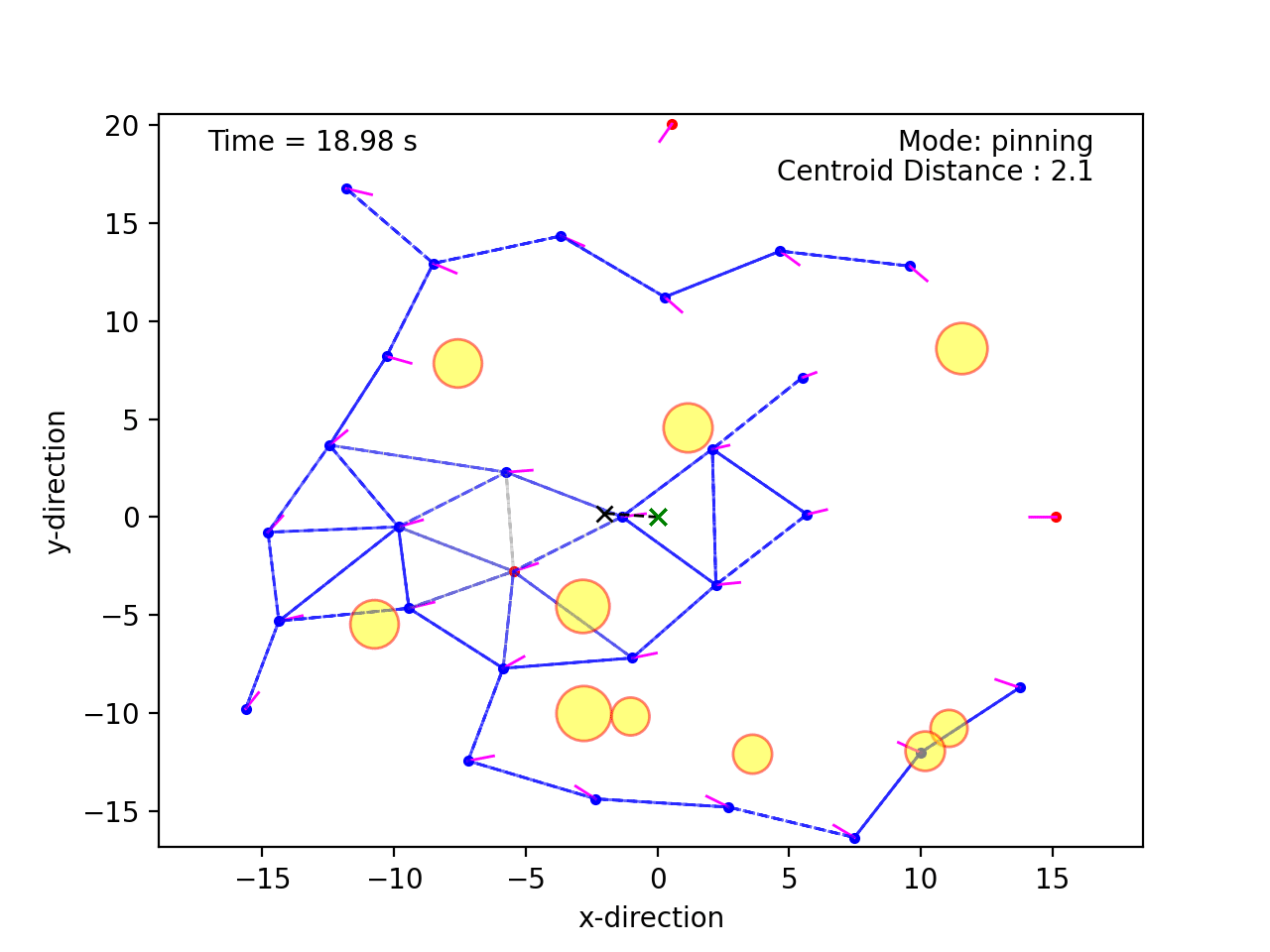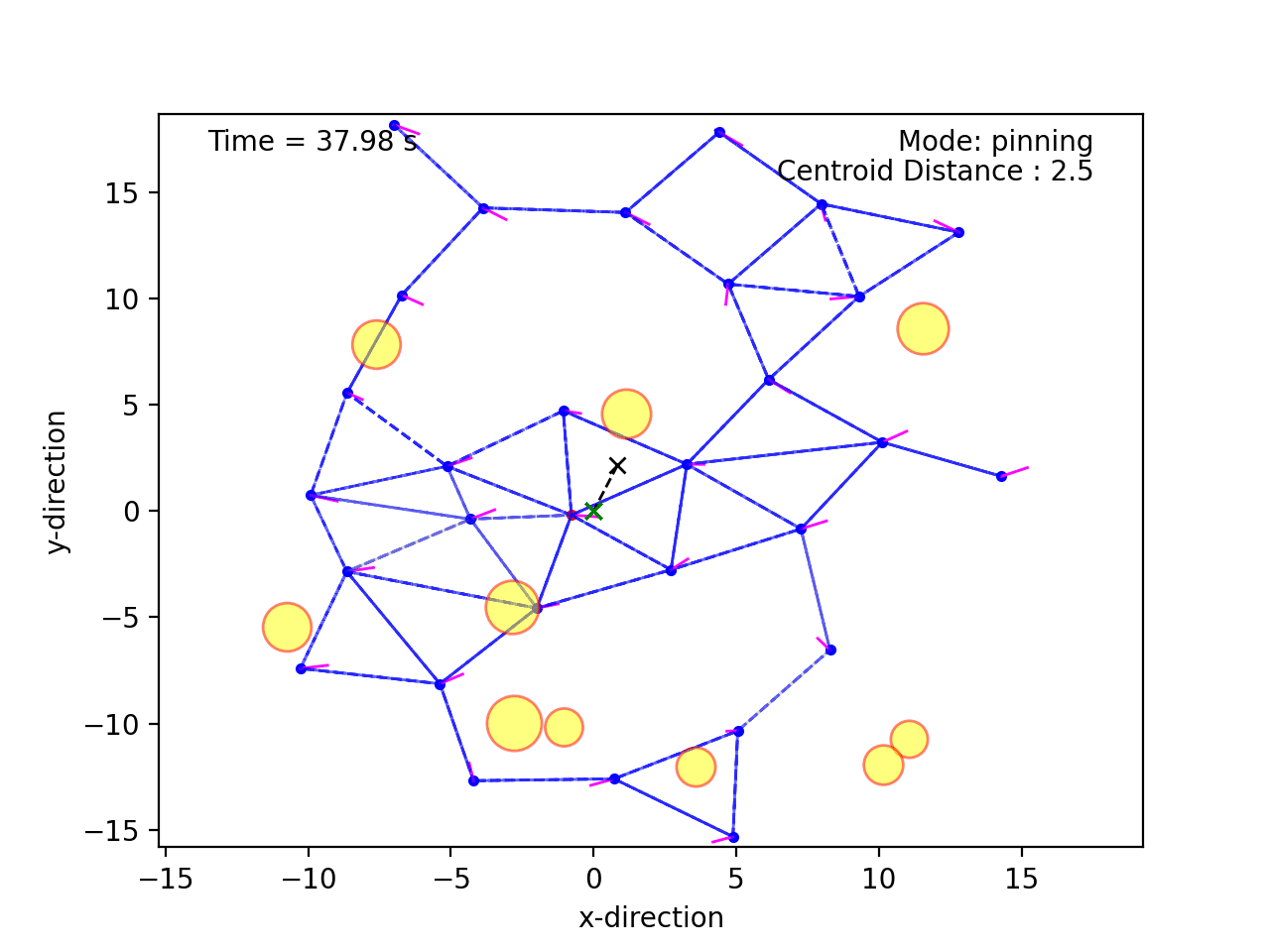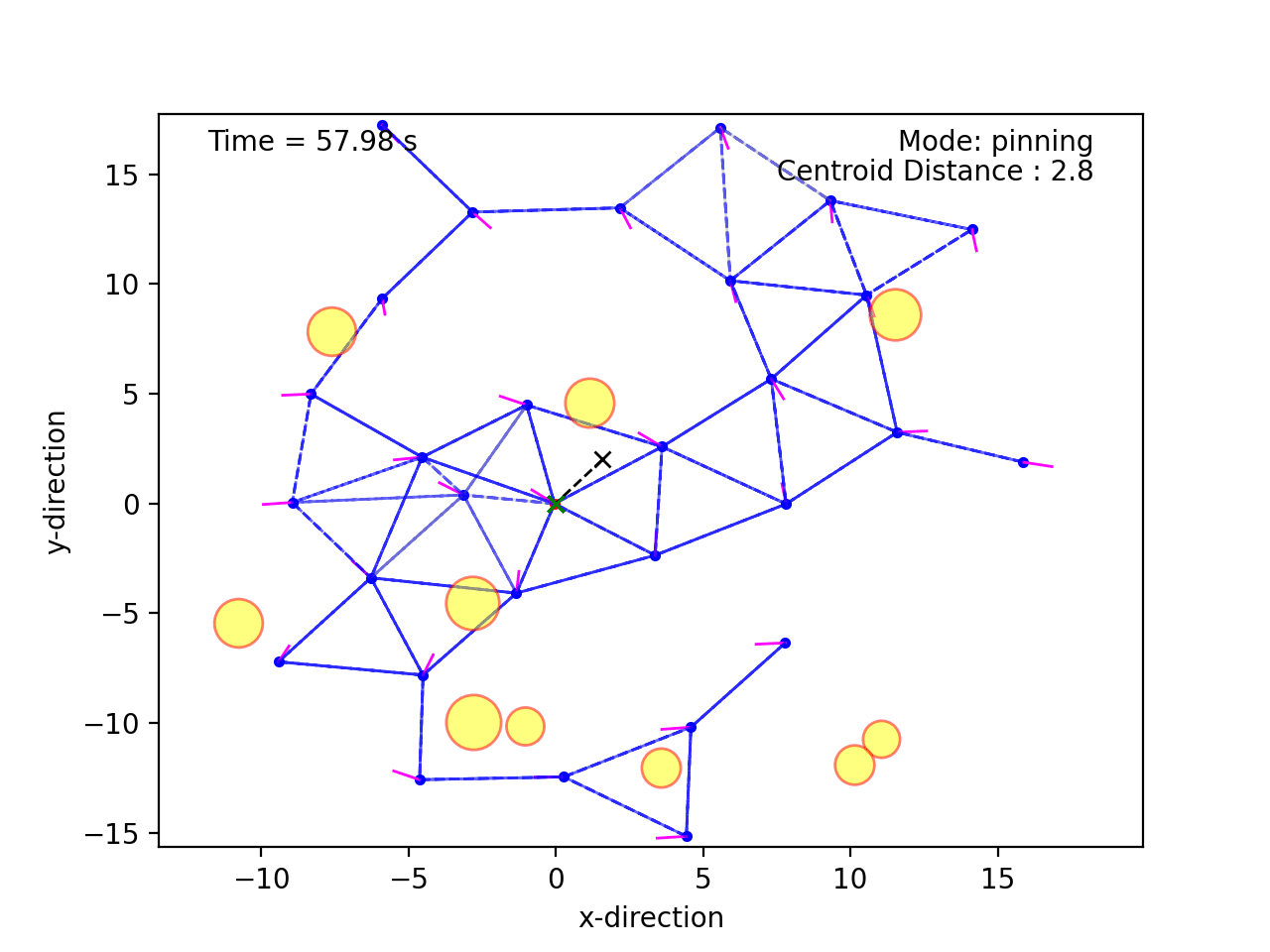
Fig. 1: Illustration of potential functions in action.

Note that the agents maintain some common distance between eachother, except when navigating around the obstacles in yellow.

Potential

A common potential function used in molecular dynamics and lattice formation with equilibrium distances is the Lennard-Jones potential function:

$$ V = \frac{a}{(|\mathbf{x}_i - \mathbf{x}_j|)^{12}} - \frac{b}{(|\mathbf{x}_i - \mathbf{x}_j|) ^6} $$

where xi and xj are the positions of agents i and j and a and b are gain parameters selected for desired performance. Notice that as the agents get closer together, the value of the a-potential decreases, while the value of b-potential increases. The idea is to select parameters that balance the need for cohesion (a) with the need to avoid collisions (b).

Gradient

We control the agents by minimizing the gradient of V over time (often through gradient descent methods). This requires us to compute the gradient as follows:

$$ \nabla V = \left( \frac{-12a}{(|\mathbf{x}_i - \mathbf{x}_j| ^{13})} + \frac{6b}{(|\mathbf{x}_i - \mathbf{x}_j|) ^7} \right) \hat{\mathbf{u}} $$

where u with the litte hat is a unit vector representing the direction from xj to xi.

Comparisons

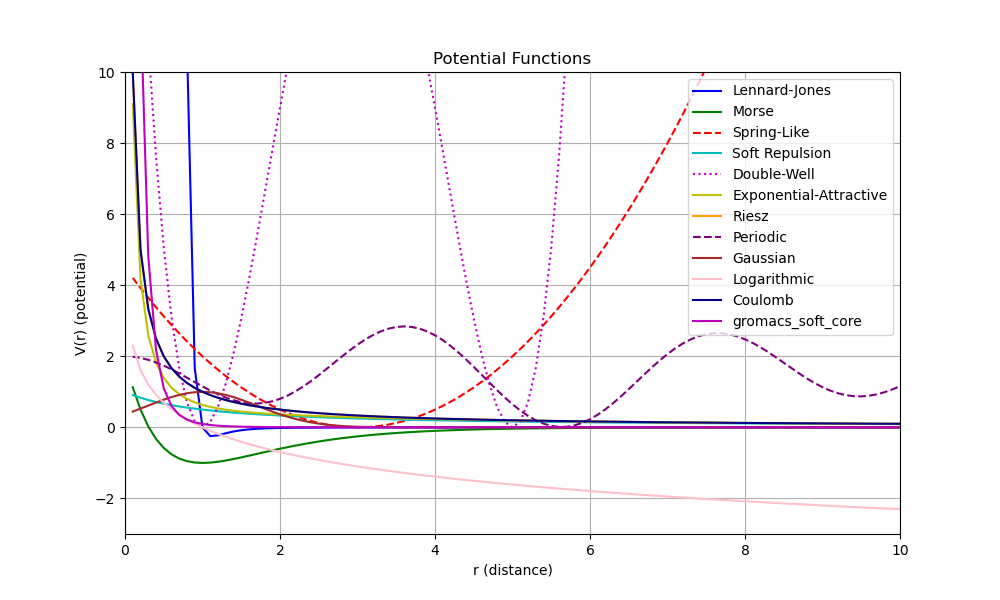
Different potential functions produce different transient and steady-state performance characteristics. Fig. 2 compares some of the more common variants.

Fig. 2: Comparison of common potential functions.

Implemention

One of the seminal works in multi-agent flocking algorithms and theory provides more sophisticated potential functions and stability analysis tailored for these applications. If you are interested in practical implementations of these and other multi-agent coordination strategies, check out my still-evolving Multiagent Coordination Simulator.

References

  1. My Survey of Potential Functions for Multi-agent Systems

  2. J. E. Jones, “On the determination of molecular fields”, Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 106(738), 441-462, 1924.

  3. Reza Olfati-Saber, “Flocking for Multi-Agent Dynamic Systems: Algorithms and Theory”, IEEE Transactions on Automatic Control, Vol. 51 (3), 2006.

  4. My Multiagent Coordination Simulator